CONTENTS
- SCIENCE TOPICS - カリウムチャネルKcsA のゲート開閉と連動した膜中集合・離散ダイナミクス (角野 歩・老木成稔) P.141~
- SCIENCE TOPICS - 視覚野の眼優位性カラムはヨザル等霊長類にかなり広く保存されている (高畑 亨・Jon H. Kaas) P.141~
- PROFILE - 平野勝也 P.143~
- AWARD - 榎木亮介 (2013 年度 日本生理学会奨励賞 ・ 2013 年度 第18 回久野寧記念賞(環境生理学GD 久野寧賞) 受賞) P.144~
- AWARD - 橋本谷祐輝 (2013 年度 日本生理学会奨励賞 受賞) P.145~
- AWARD - 風間逸郎(2013 年度 日本生理学会奨励賞 受賞) P.146~
- AWARD - 掛川 渉 (2013 年度 入澤宏・彩記念若手研究奨励賞 [イオンチャンネル・トランスポーター部門] 受賞) P.147~
- AWARD - 樽野陽幸 (2013 年度 入澤宏・彩記念若手研究奨励賞 [イオンチャンネル・トランスポーター部門] 受賞) P.148~
- AWARD - 竹内綾子 (2013 年度 入澤宏・彩記念若手研究奨励賞 [心臓・循環部門] 受賞) P.149~
- AWARD - 牛腸義宏 (2013 年度 入澤宏・彩記念JPS 優秀論文賞 受賞) P.150~
- AWARD - 木村純子 (2013 年度 入澤彩記念女性生理学者奨励賞 受賞) P.151~
- AWARD - 中村一芳 (2013 年度 細胞と分子生理/上皮膜研究グループJPS 優秀論文賞 受賞) P.152~
- AWARD - 第91 回日本生理学会 優秀ポスター賞 受賞者一覧 P.153~
- AFTERNOON TEA - 安尾敏明 「陶芸と生理学」 P.154~
- AFTERNOON TEA - 安部 力 「医療通訳セミナー」 P.154~
- CALENDAR - 主な研究集会日程 P.157~
- 特集/SYMPOSIA - 網膜神経回路研究の進歩(S08) P.159~
- 特集/SYMPOSIA - グルタミン酸シナプスの神経生物学(S14) P.159~
- 特集/SYMPOSIA - 若手研究者が切り開く食欲調節研究のフロンティア(S35) P.159~
- 特集/SYMPOSIA - 血流分布不均衡ショックと血圧調節破綻のメカニズム(S49) P.159~
- ABSTRACTS (Pt.2) - グルタミン酸シナプスの神経生物学(S14) Pt.2
- ABSTRACTS (Pt.2) - 血流分布不均衡ショックと血圧調節破綻のメカニズム(S49) Pt.2
- ABSTRACTS - 第65 回日本生理学会中国四国地方会 P.164~
- ABSTRACTS (Pt.2) - 第65 回日本生理学会中国四国地方会 (Pt.2)
- RECORDS - 第91 回日本生理学会大会を終えて P.165~
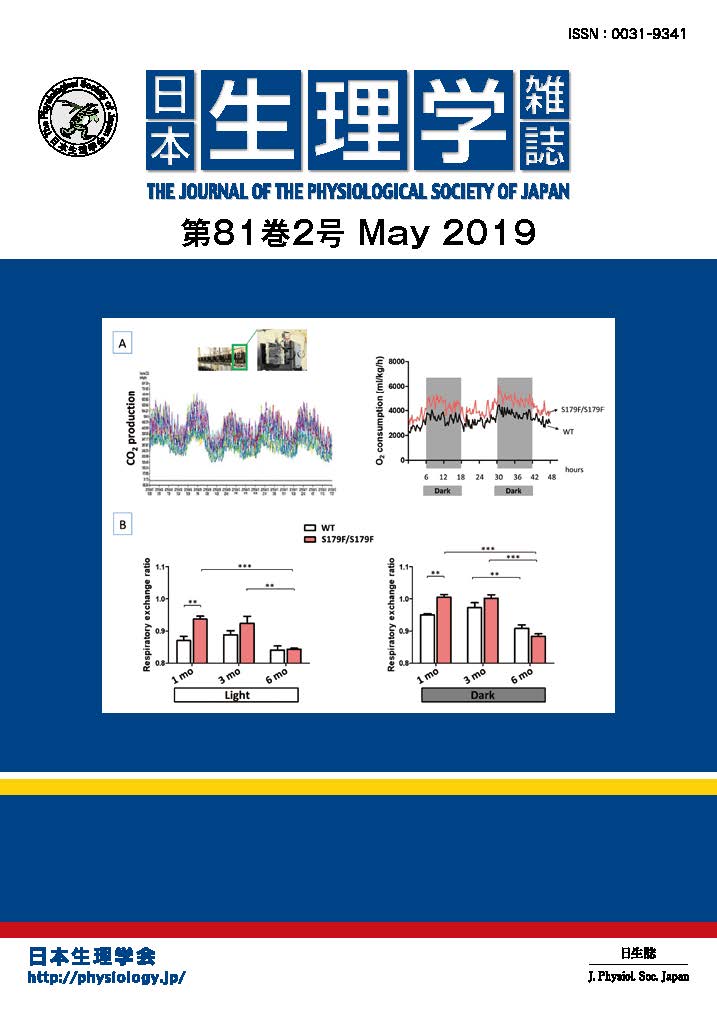
表紙の説明
演題番号:1P-054
演題名:心筋細胞の電気的活動に対する各細胞膜イオン輸送機転の寄与度(リードポテンシャル解析)
Quantifying contributions of individual ion transport mechanisms to electric activities by using cardiac myocyte models
演者: 山岡周代1,Cha ChaeYoung2,野間昭典1
所属:1 立命館大学大学院 生命科学研究科 バイオシミュレーション研究室, 2Oxford Centre for Diabetes Endocrinology and Metabolism, University of Oxford
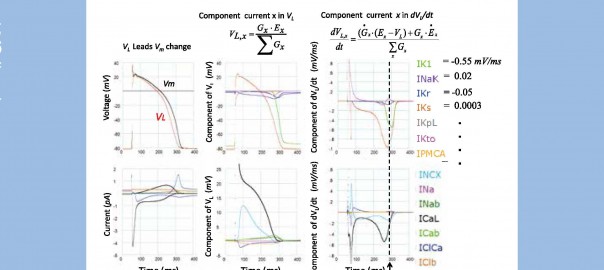
活動電位のある時点でのイオンチャネル電流(Ix)を,その瞬間のスロープコンダクタンス(Gx)と平衡電位(Ex)を用いて次の直線式で記述することができる.
(1)
この式を用いて,細胞膜全体の平衡電位(VL)は,各電流成分の和として与えられる.
(2)
ヒト心室筋活動電位モデルの再分極相についてVL(赤線)を活動電位(Vm)に重ねると分かるように(左列上図),Vm は常にVL(lead potential)を追従する.中列にはVL に占める各電流成分GxEx の大きさ(mV 単位)を示している.(2)式の微分dVL/dt もやはり右列上に示した各電流成分の和で与えられる.これによって,各電流のVL(≈Vm)変化への寄与度を定量的に表すことができる.例えば,縦点線の時点(300ms)での各コンポーネントの大きさ(mV/ms 単位)を示している.(色線は各イオン電流成分のフォント色と対応している.)このように,リードポテンシャル解析を数学モデルに適用して,膜電位変化への各電流成分の寄与を連続的に,定量的に求めることができる.